Eksponen dan Logaritma
1. Fungsi Eksponen
Bentuk bilangan an disebut sebagai bentuk perpangkatan atau eksponensial. dari bentuk bilangan tersebut dimana a disebut sebagai bilangan pokok, sedangkan n disebut bilangan pangkat atau eksponen. Adapun sifat-sifat yang berlaku dalam bilangan eksponen rasional dapat dilihat pada bentuk operasional berikut.
Contoh Soal :
Hitung hasil perpangkatan dari bilangan (0,008)2
Jawab:
2. Persamaan Eksponen
Persamaan eksponen yaitu suatu persamaan yang bilangan pokoknya berpangkat.
Bentuk-bentuk persamaan eksponen misalnya:
Bentuk-bentuk persamaan eksponen misalnya:
a. Bentuk Persamaan a^f(x)=1
misalnya suatu bilangan memiliki persamaan a^f(x)=1 dengan a>0 dan a≠1, untuk menentukan himpunan penyelesaian bentuk persamaan eksponen tersebut gunakan sifat bahwa:
a^f(x)=1 <=> f(x)=0
b. Bentuk Persamaan a^f(x)=a^p
Misalkan suatu bilangan memiliki persamaan a^f(x)=a^p, dengan a>0 dan a≠1. Himpunan bentuk penyelesaian persamaan eksponen tersebut ditentukan dengan cara melaukan persamaan pangkat antara ruas kiri dan ruas kanan. Berikut bentuk penulisannya.
a^f(x)=a^p <=> f(x) = p
c. Bentuk Persamaan a^f(x)=a^g(x)
misalkan suatu bilangan memiliki persamaan a^f(x)=a^g(x) dengan a>0 dan a≠1. Himpunan Penyelesaian persamaan eksponen tersebut ditentukan dengan cara menyamakan persamaan pangkatnya. Berikut bentuk penulisannya.
a^f(x)=a^g(x) <=> f(x) = g(x)
d. Bentuk Persamaan a^f(x)=b^f(x)
Misalkan suatu bilangan memiliki persamaan a^f(x)=b^f(x) dengan a≠1 ;a,b >0 ; a,b≠1. Himpunan penyelesaian persamaan eksponen tersebut dapat ditentukan dengan cara menyamakan f(x) = 0. Berikut bentuk penulisannya.
a^f(x)=b^f(x) <=> f(x) = 0
e. Bentuk Persamaan a^f(x)=b^g(x)
Misalkan suatu bilangan memiliki persamaan a^f(x)=b^g(x) dengan a≤b ; a,b >0 ; a,b ≠1, dan f(x) ≠ g(x). Himpunan penyelesaian persamaan eksponen tersebut dapat ditentukan dengan cara melogaritmakan kedua ruas. Berikut bentuk penulisannya.
log a^f(x)= log b^gf(x)
f. Bentuk Persamaan A{a^f(x)}² + B{a^f(x)} + C = 0
Untuk menentukan penyelesaian persamaan eksponen yang berbentuk persamaan kuadrat dapat dikerjakan dengan cara memfaktorkan, melengkapkan kuadrat sempurna atau rumus abc
g. Bentuk Persamaan f(x)^g(x) = 1; f(x)≠g(x)
Untuk menyelesaikan persamaan eksponen dengan bentuk tersebut dapat dilakukan dengan langkah-langkah berikut.
- g(x) = 0 karena ruas kanan nilainya 1 maka g(x) harus =0
- f(x) =1 karena jika f(x) = 1 maka bilangan 1 dipangkatkan berapapun nilainya tetap 1
- f(x) = -1 dengan ketentuan g(x) = harus genap
h. Bentuk Persamaan f(x)^g(x) = f(x)^h(x)
Untuk nilai g(x) ≠ h(x). Himpunan penyelesaian bentuk persamaan eksponen tersebut diperoleh dari 4 kemungkinan seperti berikut.
- g(x) = h(x) karena bilangan pokok sudah sama maka pangkat juga harus sama
- f(x) =1 karena g(x) ≠ h(x) maka bilangan pokok harus bernilai 1 agar persamaan bernilai benar
- f(x) =-1 maka g(x) dan h(x) masing-masing harus bernilai genap atau bernilai ganjil
- f(x) = 0 maka g(x) dan h(x) masing-masing bernilai positif dituliskan g(x)>0 atau h(x)>0
i. Bentuk Persamaan g(x)^f(x) = h(x)^f(x)
Persamaan ini dapat bernilai benar jika
- f(x) = 0 untuk g(x) ≠0 dan h(x)≠0
- g(x) = h(x)
2. Fungsi Logaritma
Bentuk eksponen atau perpangkatan dapat ditulis juga dalam bentuk logaritma. Penulisannya secara umum seperti berikut.
JIka ab = c dengan a>0 dan a≠1 maka alog c = b dalam hal ini disebut basis atau pokok logaritma dan c adalah bilangan yang dilogaritmakan. Berikut adalah merupakan sifat-sifat logaritma.
a. Bentuk Umum Fungsi Logaritma yaitu jika ay =x dengan a≥0 dan a≠1 maka y = alog x
Mempunyai sifat seperti berikut.
- semua x > 0 terdefinisi
- jika x mendekati 0 maka nilai y besar sekali dan positif
- bila x=1 maka y=0
- bila x>1 maka y bernilai negatif sehingga jika nilai x semakin besar maka nilai y semakin kecil
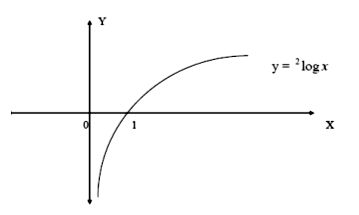
b. Grafik Fungsi y = alog x untuk a>0
Mempunyai sifat-sifat seperti berikut.
- untuk semua x>0 terdefinisi
- jika x mendekati 0 maka y bernilai kecil sekali dan negatif
- untuk x=1 maka y=0
- untuk x>1 maka y bernilai positif sehingga jika x semakin besar maka y semakin besar pula.
Berikut gambar grafiknya:
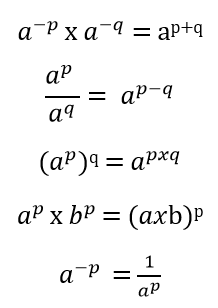
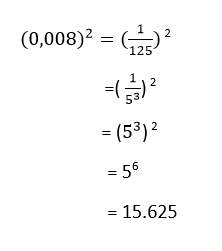
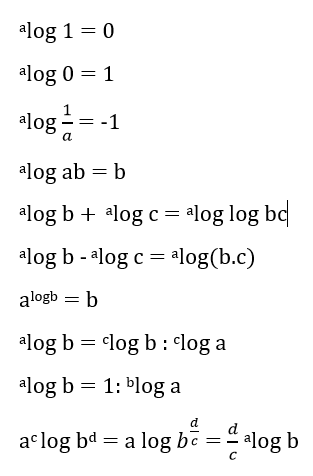






0 Comments:
Posting Komentar